encryption: the fated story of alice and bob

#math #numbertheory #cryptography

Today's world runs on data. We’ve generated more data in the past two years than in our entire history combined. This data revolution has also allowed us to communicate more than ever before. Humanity revolves around communication, especially private communication — but how do we keep communication data private?

Gone are the days where spies secretly exchanged envelopes with secret codes in them at a nondescript park bench. Gone are the days of the Enigma machine and substitution ciphers. Encryption has evolved quite a bit, and it holds some very interesting math. I love math, and the math involved in encryption is very elegant — and very clever.

what is encryption?

The goal of encryption is to take a message (in plain text) and scramble it so no one except the person you want to send the message to can read it. To understand this better, let’s take the example of the immortal Alice and Bob.

Alice is madly in love with Bob, and she wants to tell him. However, she doesn’t want anyone else to know, just in case Bob doesn’t love her back. How can she send the message to Bob?

One way would be to use a simple 1-to-1 encoding system — we map each character to another character and encrypt the message. Let’s say a=1, b=2 and so on. Hence:

'i love you' = 9 0 12 15 ...

Cool! Alice now has a nice, garbled message that no one can read! The only problem, of course, is that Bob can’t read it either. How does she tell Bob how to decrypt the message? Simple encryption schemes like this fail because there is no way to send the common key without using a more advanced encryption system. If Alice tries to encrypt the key, then the key to that key has to be sent too. So unless Alice is willing to pluck up the courage to talk to Bob in-person (secretly at a nondescript park bench of course), she can’t encrypt her message in such a simple way.

This is how kids make “secret codes”. Both parties have to be in on the cipher for it to work, but this throws us into the realm of paradox.

Public-key encryption introduces asymmetry to a simple cipher system. The idea is that the key used to encrypt the message is different from the key used to decrypt the message. Public-key encryption is notoriously difficult to wrap one’s head around, but I’ll try my best to explain. Here’s one analogy that I find helpful:

Imagine both Alice and Bob have a mailbox. Each mailbox has 2 different locks. One lock opens a small slot to put letters in, and the other opens the entire mailbox for mail to be taken out.

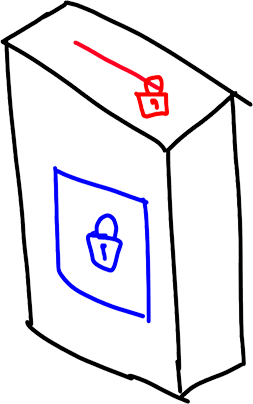
The principle of public-key encryption is that everyone has the key used to encrypt messages (i.e. put mail through the red slot). This means that Bob has made many copies of the red key, and has even left a red key on top of the mailbox. However, only Bob has the blue key that is needed to actually see Bob’s mail. Thus, for Alice to send a secret message all she would have to do was encrypt it using Bob’s public key, and no one would be able to decipher it except Bob.

That’s how RSA encryption works.

Let’s turn this into a more formal definition. Public key encryption revolves around an asymmetric system with two keys. The keys are related in such that a message encrypted by one key can only be decrypted with the other key. However, the keys cannot be derived from one another (we’ll get into that later). One of these keys is designated as the public key, and the other is the private key. The private key is never shared with anyone except its owner. The public key is available for everyone to see.

This is great for sending encrypted messages, but it has some other interesting applications. For example, say Alice uses her private key to encrypt the message. When she sends it, anyone can decrypt it using her public key — but the fact that it can be decrypted by her private key means that it was definitely Alice who sent that message. Alice can even encrypt using her private key and then Bob’s public key after that! This would mean that only Bob can see the message, but he knows that Alice sent it.

This is where it can start to get a little confusing to just deal with Alice and Bob. Here’s a Star Wars analogy with something a little more concrete.

In Episode IV, Princess Leia needs to send a message to Obi-Wan Kenobi.

help me obi-wan kenobi! you're my only hope.
signed, leia

She uses her private key to encrypt this message and then uses Obi-Wan’s public key to encrypt in once again. She puts it in our friend R2-D2, who successfully delivers it to Obi-Wan. Obi-Wan decrypts this with his private key. Now he sees the garbled mess of a message, so he can’t read it. The last step he has to do is decrypt the message one more time with Leia’s public key, confirming that this message is definitely from Leia.

This is a concept known as “signing”. It adds a layer of identity verification, where otherwise anyone could claim to Leia.

ok ok, i get it. but how does it work?

When I first learned about encryption, it drove me absolutely mad. I perfectly understood the whole public/private key system, but I just couldn’t wrap my head around how the actual messages get garbled, why we could be sure the keys couldn’t be derived from each other, and how the messages actually get scrambled. It turns out it’s non-trivial but very clever. If you’d rather not go through a lot of math, then I suggest you move on now. I think all of this is super interesting, so let’s dive in.

RSA works, as we said, on a system of 2 keys: public and private. The public key is represented by two integers: $n$ and $e$ (not Euler's $e$). The private key is represented by $d$. We’re going to be using some interesting mathematical notation later on, but I’ll explain as we encounter it.

At a fundamental level, RSA is an algorithm. That means we have steps that we need to follow.

Choose 2 prime numbers, $p$ and $q$.

This might seem hard, but prime numbers are pretty common. We also have blazingly fast algorithms to test if a number is prime (called primality tests), so finding primes isn’t that hard. For security, $p$ and $q$ should be chosen randomly. They are also very big primes, but for the sake of this example, we’ll keep them fairly small.

Next, we calculate $n$ as the product of $p$ and $q$. In sum:

Choose $2$ primes $p$ and $q$, and let $n=pq$. WLOG let $p=5$ and $q=7$, so $n=35$. Cool? Great.

Now we take the totient of $n$. Euler’s totient function is a function that returns the number of numbers that are coprime to $n$ that are less than $n$. For example, $\varphi(6)=1$, the only coprime number being $5$. Coprime means that two numbers share no factors other than $1$.

In our case, we have that

This should make intuitive sense. $n$ is the product of two primes $p$ and $q$, so the totient only rejects the $q$ multiples of $p$ and the $p$ multiples of $q$. This doublecounts $pq$, so we add $1$ to correct for that. So in our example, we have

Now we choose $e$ with the following conditions:

For our example, $e=5$ works.

Finally, we need to find $d$. $d$ needs to satisfy the condition

Now we're into it! This is modular arithmetic. You can think of it as "math on a clock"; we're treating all integers as equivalent (or congruent) to their remainders (or residues) when divided by a number. For example, $5 = 4+1$, so $5 \equiv 1\mod 4$. We can also add, subtract, and multiply numbers as normal (try and prove these!). Division is more complicated, so I'll let you explore that. Some examples:

We can also have negative moduli, as shown in the last line. The reason this is typically useful is to simplify computations. For example, say we want to find the remainder when $25 \cdot 1294$ is divided by $7$. We could do the entire multiplication and then divide, or we could reduce first like so:

We know that $21$ and $1918$ are both divisible by $7$, so they leave behind $0$. Thus we have

Later, we're going to use raise numbers to big numbers in a modulus to encrypt, so this kind of reduction is going to save us a lot of computation.

Now, recall that we're trying to find $d$ such that $de \equiv 1 \mod \varphi(n)$. In our particular example, we know $e=5$ and $\varphi(n) = 24$, so just by inspection we can find $d=5$ works. Once again, we're glossing over some technical details on how to find this in general. Check out Extended Euclidean Algorithm to learn more.

Some of this might feel arbitrarily defined at the moment — trust in the Force, this'll all come together soon.

To recap, we have now found both the private and public keys. $d$ is the private key, so we have to keep that secret. $p$, $q$ and $\varphi(n)$ also have to be kept secret, since they are used in the derivation of $d$. More rigorously: given any of those values, $d$ can be calculated with the already public $e$. In fact, these numbers can just be discarded once $d$ is calculated, and they often are — why have more risk?

Notice that while creating a private key is very easy, deriving the private key from a public key is very, very hard. The only way to do so is to find the prime factors $p$ and $q$ — this is a notoriously hard problem. It’s like mixing two paints and then trying to derive the exact colours of paint used in just the right proportions.

let’s encrypt a message!

The first step is to take this plain text and convert it into a sequence of numbers. Let’s use a simple encoding system, where $a=1$, $b=2$ and so on. To be clear, this step isn’t to make the message harder to read, it’s just so that we can perform mathematical operations on the text. Astute among you might realize that we can also just use ASCII encoding to get the numbers:)

HELLO THERE = [8, 5, 12, 12, 15, 0, 20, 8, 5, 18, 5]

Let’s say Obi-Wan is trying to get a message to Master Yoda. He has his text in numbers, so the next step is to encrypt! He needs to use Yoda’s public key, which we’ll say is the example we worked above. He raises all the numbers to the power of $e$, giving [32768, 3125, 248832, 248832, 759375, 0, 3200000, 32768, 3125, 1889568, 3125]

Now he'll take all those numbers $\mod n$. This is where that computational efficiency comes in: instead of computing these huge numbers, we can just spin the hands on the clock. That is, we can reduce whenever we can to make the numbers smaller, making the computation much faster.

   [32768, 3125, 248832, 248832, 759375, 0, 3200000, 32768, 3125, 1889568, 3125]
=> [8, 10, 17, 17, 15, 0, 20, 8, 10, 23, 10]
=> 'HJQQO THJWJ'

Nonsense! Now Obi-Wan sends this to Master Yoda. Yoda has his private key $d$, which will give us the right message back. We raise the numbers to the power $d$ and take $\mod n$ again, and voila!

   [8, 10, 17, 17, 15, 0, 20, 8, 10, 23, 10]
=> [32768, 100000, 1419857, 1419857, 759375, 0, 3200000, 32768, 100000, 6436343, 100000]
=> [8, 5, 12, 12, 15, 0, 20, 8, 5, 18, 5]
=> 'hello there'

Yay! Although it would've been less work to just use the Force...

Let's abstractify this a bit. Let the message be $M$. $M$ could be a number or a list of numbers, but for now we can just treat it as a number. To take this to a list, we can just do these operations elementwise like we did above.

Let $\alpha$ and $\beta$ be the encryption and decryption function respectively. We have

We dropped the mods, but all of this is happening $\mod n$. Letting $M'$ be the encrypted message, so $M' = \alpha(M) = M^e$. Now we have

Recall that $de=1 \mod n$, hence

So our encryption and decryption reverse each other, like we expected. The key idea is that we spin the clock by raising to the $d$-th. The only way to figure out how to undo this operation is by factoring $n$, as we discussed earlier.

caveats

Before we move on, it’s important to know that this is a simplified version. RSA uses a different function called Carmichael’s totient function instead of Euler’s totient function. Euler’s function is still mathematically sound, but in some cases, it generates larger numbers than necessary. Carmichael’s totient function fixes that.

There are also a couple of problems that our basic algorithm has. For one, using small e makes this very weak. Our small choices for $p$ and $q$ make it weak already, but this is different. If you have a small integer value for the message, the encrypted message will just be the message $m$ to the power $e$. This can easily be broken just by taking the $e$-th root of the encrypted message. Once $e$ gets past a certain threshold, however, it becomes impossible to decrypt without the private key.

Our basic RSA is also completely deterministic, in that if you put the same text in, you will get the same encryption out. This makes it vulnerable to chosen-ciphertext attacks. If you’re interested, read this.

To combat this, actual implementations of RSA employ random padding, where a message is randomly padded to make it semantically secure (i.e. the encryption is a bit different every time).

It’s also very important to understand that while our public and private keys were the same in this case, normally this wouldn’t be so. Since our numbers are small, we’re limited in our choices.

And, for the final note, we have to talk about quantum. Shor’s algorithm (an algorithm I’d like to write about in the future) makes factoring really big numbers trivial, and thus completely breaks this RSA system. However, as of right now and for the foreseeable future, quantum computers are nowhere close to being able to factor the massive 2048-bit integers that are commonly in use today. Besides, we have other cryptographic systems (that I will hopefully discuss in the future) that are more resistant to the quantum revolution.

and that’s it!

Thanks so much for reading! Here are some key takeaways:

• Encryption is all about garbling messages in such a way that only the intended reader can read it
• Simple key-based ciphers can be easily broken since the key itself needs to be transmitted securely as well
• Public-key encryption solves this by having two keys, public and private
• The public key encrypts information so that only the private key (which is only known by the intended target) can decrypt it
• RSA is an algorithm, based around concepts in number theory
• The mathematical operations performed in RSA encryption can only be reversed by the private key
• The private key can only be found by breaking down a product of 2 very big primes into its factors — something that we have yet to do efficiently